2 Data preparation

2.1 Load data

The data required for ditigal soil mapping are:

Soil samples of variables measured in the field. These observations need to be geo-located and are used as the target for the model that is then used for spatial upscaling.
Environmental covariates, provided as geospatial raster maps. These covariates act as predictors in the model that is used for spatial upscaling.

Let’s load them

2.1.1 Soil samples

Code

# Load soil data from sampling locations
df_obs <- readr::read_csv(
  here::here("data-raw/soildata/berne_soil_sampling_locations.csv")
  )

# Display data
head(df_obs) |> 
  knitr::kable()

site_id_unique	timeset	x	y	dataset	dclass	waterlog.50	waterlog.100	ph.0.10	ph.10.30	ph.30.50	ph.50.100
4_26-In-005	d1968_1974_ptf	2571994	1203001	validation	poor	0	1	6.071733	6.227780	7.109235	7.214589
4_26-In-006	d1974_1978	2572149	1202965	calibration	poor	1	1	6.900000	6.947128	7.203502	7.700000
4_26-In-012	d1974_1978	2572937	1203693	calibration	moderate	1	1	6.200000	6.147128	5.603502	5.904355
4_26-In-014	d1974_1978	2573374	1203710	validation	well	0	0	6.600000	6.754607	7.200000	7.151129
4_26-In-015	d1968_1974_ptf	2573553	1203935	validation	moderate	0	1	6.272715	6.272715	6.718392	7.269008
4_26-In-016	d1968_1974_ptf	2573310	1204328	calibration	poor	0	1	6.272715	6.160700	5.559031	5.161655

The dataset on soil samples from Bern holds 13 variables for 1052 entries (more information here):

site_id_unique: The location’s unique site id.
timeset: The sampling year and information on sampling type for soil pH (no label: CaCl\(_2\) laboratory measurement, field: indicator solution used in field, ptf: H\(_2\)O laboratory measurement transferred by pedotransfer function).
x: The x (easting) coordinates in meters following the (CH1903/LV03) system.
y: The y (northing) coordinates in meters following the (CH1903/LV03) system.
dataset: Specification whether a sample is used for model training ("calibration") or testing ("validation") (this is based on randomization to ensure even spatial coverage).
dclass: Soil drainage class
waterlog.30, waterlog.50, waterlog.100: Specification whether soil was water logged at 30, 50, or 100 cm depth (0 = No, 1 = Yes).
ph.0.10, ph.10.30, ph.30.50, ph.50.100: Average soil pH between 0-10, 10-30, 30-50, and 50-100 cm depth.

2.1.2 Environmental covariates

Now, let’s load the covariates that we want to produce our soil maps with. These files are in the geoTIFF format - geolocated TIFF files.

Code

# Get a list with the path to all raster files
list_raster <- list.files(
  here::here("data-raw/geodata/covariates/"),
  full.names = TRUE
  )

# Display data (lapply to clean names)
lapply(
  list_raster, 
  function(x) sub(".*/(.*)", "\\1", x)
  ) |> 
  unlist() |> 
  head(5) |> 
  print()

[1] "NegO.tif"         "PosO.tif"         "Se_MRRTF2m.tif"   "Se_MRVBF2m.tif"  
[5] "Se_NO2m_r500.tif"

The output above shows the first five raster files with rather cryptic names. The meaning of all 91 raster files are given in Chapter 6. Make sure to have a look at that list as it will help you to interpret your model results later on. Let’s look at one of these raster files, Se_slope2m.tif, to get a better understanding for our data. That file contains the local slope of the terrain, derived from a digital elevation model with 2 m resolution:

Code

# Load a raster file as example: Picking the slope profile at 2 m resolution
raster_example <- terra::rast(
  here::here("data-raw/geodata/covariates/Se_slope2m.tif")
  )
raster_example

class       : SpatRaster 
dimensions  : 986, 2428, 1  (nrow, ncol, nlyr)
resolution  : 20, 20  (x, y)
extent      : 2568140, 2616700, 1200740, 1220460  (xmin, xmax, ymin, ymax)
coord. ref. : CH1903+ / LV95 
source      : Se_slope2m.tif 
name        : Se_slope2m 
min value   :    0.00000 
max value   :   85.11286

As shown in the output, a raster object has the following properties (among others, see ?terra::rast):

class: The class of the file, here a SpatRaster.
dimensions: The number of rows, columns, years (if temporal encoding).
resolution: The resolution of the coordinate system, here it is 20 in both axes.
extent: The extent of the coordinate system defined by min and max values on the x and y axes.
coord. ref.: Reference coordinate system. Here, the raster is encoded using the LV95 geodetic reference system from which the projected coordinate system CH1903+ is derived.
source: The name of the source file.
names: The name of the raster file (mostly the file name without file-specific ending)
min value: The lowest value of all cells.
max value: The highest value of all cells.

Tip

The code chunks filtered for a random sub-sample of 15 variables. As described in Chapter 5, your task will be to investigate all covariates and find the ones that can best be used for your modelling task.

2.2 Visualise data

Now, let’s look at a visualisation of this raster file. Since we have selected the slope at 2 m resolution, we expect a relief-like map with a color gradient that indicates the steepness of the terrain. A quick way to look at a raster object is to use the generic plot() function.

Code

# Plot raster example
terra::plot(raster_example)

To have more flexibility with visualising the data, we can use the ggplot() in combination with the {tidyterra} package.

Code

library(tidyterra)

# To have some more flexibility, we can plot this in the ggplot-style as such:
ggplot2::ggplot() +
  tidyterra::geom_spatraster(data = raster_example) +
  ggplot2::scale_fill_viridis_c(
    na.value = NA,
    option = "magma",
    name = "Slope (%) \n"
    ) +
  ggplot2::theme_bw() +
  ggplot2::scale_x_continuous(expand = c(0, 0)) +  # avoid gap between plotting area and axis
  ggplot2::scale_y_continuous(expand = c(0, 0)) +
  ggplot2::labs(title = "Slope of the Study Area")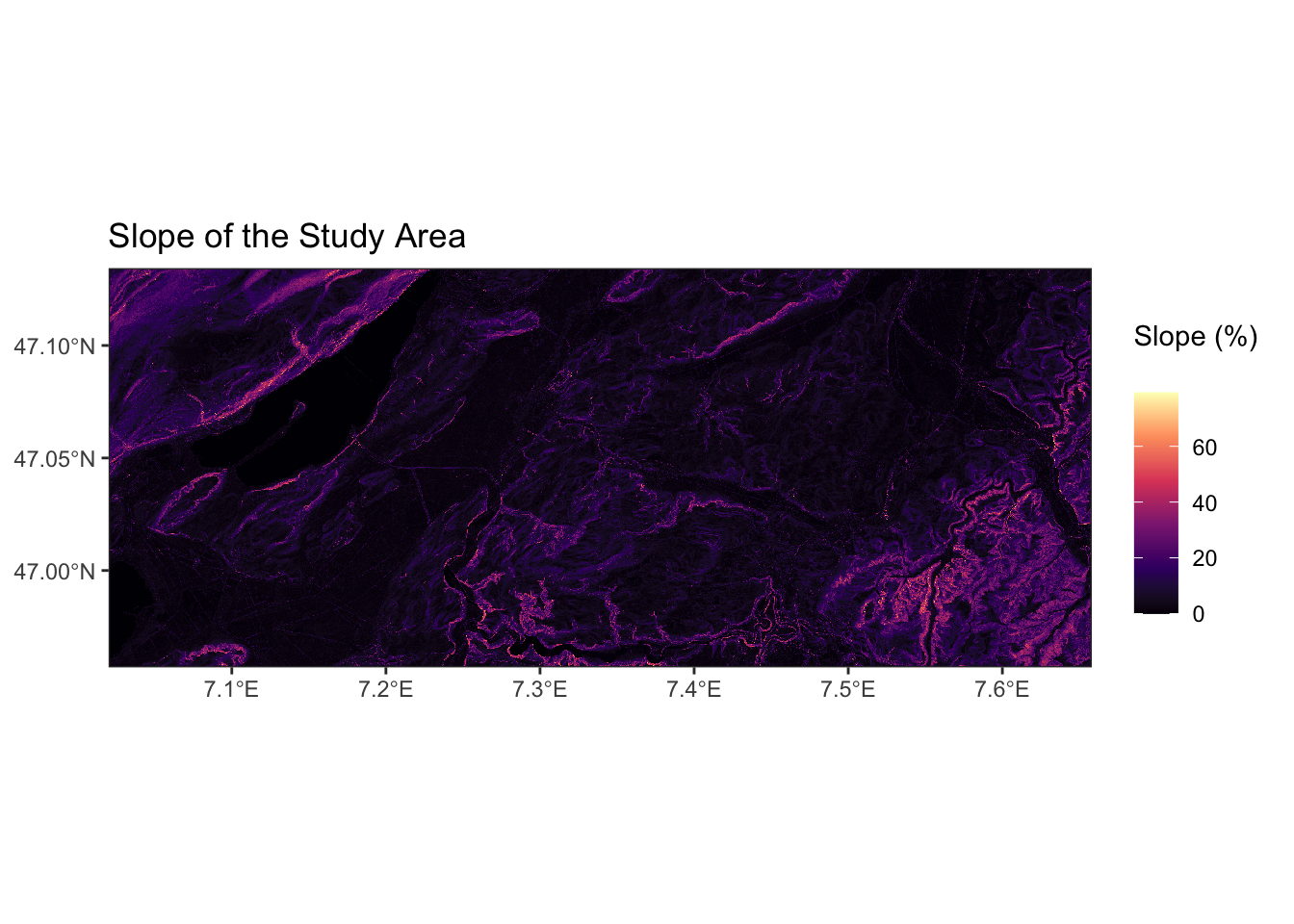

Tip

Note that the second plot has different coordinates than the upper one. That is because the data was automatically projected to the World Geodetic System (WGS84, ESPG: 4326).

This looks already interesting but we can put our data into a bit more context. For example, a larger map background would be useful to get a better orientation of our location. Also, it would be nice to see where our sampling locations are and to differentiate these locations by whether they are part of the training or testing dataset. Bringing this all together requires some more understanding of plotting maps in R. So, don’t worry if you do not understand everything in the code chunk below and enjoy the visualizations:

Code

# To get our map working correctly, we have to ensure that all the input data
# is in the same coordinate system. Since our Bern data is in the Swiss 
# coordinate system, we have to transform the sampling locations to the 
# World Geodetic System first.
# To look up EPSG Codes: https://epsg.io/
# World Geodetic System 1984:  4326
# Swiss CH1903+ / LV95: 2056

# For the raster:
rasta <- terra::project(raster_example, "+init=EPSG:4326")

# Let's make a function for transforming the sampling locations:
change_coords <- function(data, from_CRS, to_CRS) {
  
  # Check if data input is correct
  if (!all(names(data) %in% c("id", "lat", "lon"))) {
    stop("Input data needs variables: id, lat, lon")
  }
  
  # Create simple feature for old CRS
  sf_old_crs <- sf::st_as_sf(data, coords = c("lon", "lat"), crs = from_CRS)
  
  # Transform to new CRS
  sf_new_crs     <- sf::st_transform(sf_old_crs, crs = to_CRS)
  sf_new_crs$lat <- sf::st_coordinates(sf_new_crs)[, "Y"]
  sf_new_crs$lon <- sf::st_coordinates(sf_new_crs)[, "X"]
  
  sf_new_crs <- sf_new_crs |> dplyr::as_tibble() |> dplyr::select(id, lat, lon)
  
  # Return new CRS
  return(sf_new_crs)
}

# Transform dataframes
coord_train <- df_obs |> 
  dplyr::filter(dataset == "calibration") |> 
  dplyr::select(site_id_unique, x, y) |> 
  dplyr::rename(id = site_id_unique, lon = x, lat = y) |> 
  change_coords(
    from_CRS = 2056, 
    to_CRS = 4326
    )

coord_test <- df_obs |> 
  dplyr::filter(dataset == "validation") |> 
  dplyr::select(site_id_unique, x, y) |> 
  dplyr::rename(id = site_id_unique, lon = x, lat = y) |> 
  change_coords(
    from_CRS = 2056, 
    to_CRS = 4326
    )

Code

# Notes: 
# - This code may only work when installing the development branch of {leaflet}:
# remotes::install_github('rstudio/leaflet')
# - You might have to do library(terra) for R to find functions needed in the backend
library(terra)

# Let's get a nice color palette now for easy reference
pal <- leaflet::colorNumeric(
  "magma",
  terra::values(r),
  na.color = "transparent"
  )

# Next, we build a leaflet map
leaflet::leaflet() |> 
  # As base maps, use two provided by ESRI
  leaflet::addProviderTiles(leaflet::providers$Esri.WorldImagery, group = "World Imagery") |>
  leaflet::addProviderTiles(leaflet::providers$Esri.WorldTopoMap, group = "World Topo") |>
  # Add our raster file
  leaflet::addRasterImage(
    rasta,
    colors = pal,
    opacity = 0.6,
    group = "raster"
    ) |>
  # Add markers for sampling locations
  leaflet::addCircleMarkers(
    data = coord_train,
    lng = ~lon,  # Column name for x coordinates
    lat = ~lat,  # Column name for y coordinates
    group = "training",
    color = "black"
  ) |>
    leaflet::addCircleMarkers(
    data = coord_test,
    lng = ~lon,  # Column name for x coordinates
    lat = ~lat,  # Column name for y coordinates
    group = "validation",
    color = "red"
  ) |>
  # Add some layout and legend
  leaflet::addLayersControl(
    baseGroups = c("World Imagery","World Topo"),
    position = "topleft",
    options = leaflet::layersControlOptions(collapsed = FALSE),
    overlayGroups = c("raster", "training", "validation")
    ) |>
  leaflet::addLegend(
    pal = pal,
    values = terra::values(r),
    title = "Slope (%)")

Note

This plotting example is based to the one shown in the AGDS 2 tutorial “Handful of Pixels” on phenology. More information on using spatial data in R can be found there in the Chapter on Geospatial data in R.

That looks great! At a first glance, it is a bit crowded but once you zoom in, you can investigate our study area quite nicely. You can check whether the slope raster file makes sense by comparing it against the base maps. Can you see how cliffs along the Aare river, hills, and even gravel quarries show high slope values. We also see that our testing dataset is randomly distributed across the area covered by the training dataset.

2.3 Combine data

Now that we have played with a few visualizations, let’s get back to preparing our data. The {terra} package comes with the very useful tool to stack multiple rasters on top of each other if they share the spatial grid (extent and resolution). To do so, we just have to feed in the vector of file names list_raster:

Code

# Load all files as one batch
all_rasters <- terra::rast(list_raster)
all_rasters

class       : SpatRaster 
dimensions  : 986, 2428, 91  (nrow, ncol, nlyr)
resolution  : 20, 20  (x, y)
extent      : 2568140, 2616700, 1200740, 1220460  (xmin, xmax, ymin, ymax)
coord. ref. : CH1903+ / LV95 
sources     : NegO.tif  
              PosO.tif  
              Se_MRRTF2m.tif  
              ... and 88 more source(s)
names       :      NegO,      PosO, Se_MRRTF2m, Se_MRVBF2m, Se_NO2m_r500, Se_PO2m_r500, ... 
min values  : 0.8109335, 0.8742412,   0.000000,   0.000000,    0.2755551,    0.3541574, ... 
max values  : 1.5921584, 1.6218545,   6.965698,   7.991423,    1.6376855,    1.6430260, ...

Note that above, we have stacked only a random of all available raster data (list_raster) which we have generated previously.

Now, we do not want to have the covariates’ data from all cells in the raster file. Rather, we want to reduce our stacked rasters to the x and y coordinates for which we have soil sampling data. We can do this using the terra::extract() function. Then, we want to merge the two dataframes of soil data and covariates data by their coordinates. Since number of rows and the order of the covariate data is the same as the “Bern data” (soil samples), we can simply bind their columns with cbind():

Code

# Extract coordinates from sampling locations
sampling_xy <- df_obs |> 
  dplyr::select(x, y)

# From all rasters, extract values for sampling coordinates
df_covars <- terra::extract(
  all_rasters,  # The raster we want to extract from
  sampling_xy,  # A matrix of x and y values to extract for
  ID = FALSE    # To not add a default ID column to the output
  )

df_full <- cbind(df_obs, df_covars)
head(df_full) |> 
  knitr::kable()

site_id_unique	timeset	x	y	dataset	dclass	waterlog.50	waterlog.100	ph.0.10	ph.10.30	ph.30.50	ph.50.100	NegO	PosO	Se_MRRTF2m	Se_MRVBF2m	Se_NO2m_r500	Se_PO2m_r500	Se_SAR2m	Se_SCA2m	Se_TWI2m	Se_TWI2m_s15	Se_TWI2m_s60	Se_alti2m_std_50c	Se_conv2m	Se_curv25m	Se_curv2m	Se_curv2m_fmean_50c	Se_curv2m_fmean_5c	Se_curv2m_s60	Se_curv2m_std_50c	Se_curv2m_std_5c	Se_curv50m	Se_curv6m	Se_curvplan25m	Se_curvplan2m	Se_curvplan2m_fmean_50c	Se_curvplan2m_fmean_5c	Se_curvplan2m_s60	Se_curvplan2m_s7	Se_curvplan2m_std_50c	Se_curvplan2m_std_5c	Se_curvplan50m	Se_curvprof25m	Se_curvprof2m	Se_curvprof2m_fmean_50c	Se_curvprof2m_fmean_5c	Se_curvprof2m_s60	Se_curvprof2m_s7	Se_curvprof2m_std_50c	Se_curvprof2m_std_5c	Se_curvprof50m	Se_diss2m_50c	Se_diss2m_5c	Se_e_aspect25m	Se_e_aspect2m	Se_e_aspect2m_5c	Se_e_aspect50m	Se_n_aspect2m	Se_n_aspect2m_50c	Se_n_aspect2m_5c	Se_n_aspect50m	Se_n_aspect6m	Se_rough2m_10c	Se_rough2m_5c	Se_rough2m_rect3c	Se_slope2m	Se_slope2m_fmean_50c	Se_slope2m_fmean_5c	Se_slope2m_s60	Se_slope2m_s7	Se_slope2m_std_50c	Se_slope2m_std_5c	Se_slope50m	Se_slope6m	Se_tpi_2m_50c	Se_tpi_2m_5c	Se_tri2m_altern_3c	Se_tsc10_2m	Se_vrm2m	Se_vrm2m_r10c	be_gwn25_hdist	be_gwn25_vdist	cindx10_25	cindx50_25	geo500h1id	lgm	lsf	mrrtf25	mrvbf25	mt_gh_y	mt_rr_y	mt_td_y	mt_tt_y	mt_ttvar	protindx	terrTextur	tsc25_18	tsc25_40	vdcn25	vszone
4_26-In-005	d1968_1974_ptf	2571994	1203001	validation	poor	0	1	6.071733	6.227780	7.109235	7.214589	1.569110	1.534734	5.930607	6.950892	1.562085	1.548762	4.000910	16.248077	0.0011592	0.0032796	0.0049392	0.3480562	-40.5395088	-0.0014441	-1.9364884	-0.0062570	0.0175912	0.0002296	2.9204133	1.1769447	0.0031319	-0.5886537	-0.0042508	-1.0857303	-0.0445323	-0.0481024	-0.0504083	-0.1655090	1.5687343	0.6229440	0.0007920	-0.0028067	0.8507581	-0.0382753	-0.0656936	-0.0506380	-0.0732220	1.6507173	0.7082230	-0.0023399	0.3934371	0.1770810	-0.9702092	-0.5661940	-0.7929600	-0.9939429	-0.2402939	-0.2840056	-0.6084610	-0.0577110	-0.7661251	0.3228087	0.2241062	0.2003846	1.1250136	0.9428899	0.6683306	0.9333237	0.7310556	0.8815832	0.3113754	0.3783818	0.5250366	-0.0940372	-0.0583917	10.319408	0.4645128	0.0002450	0.000125	234.39087	1.2986320	-10.62191	-6.9658718	6	7	0.0770846	0.0184651	4.977099	1316.922	9931.120	58	98	183	0.0159717	0.6248673	0.3332805	1.784737	65.62196	6
4_26-In-006	d1974_1978	2572149	1202965	calibration	poor	1	1	6.900000	6.947128	7.203502	7.700000	1.568917	1.533827	5.984921	6.984581	1.543384	1.558683	4.001326	3.357315	0.0139006	0.0070509	0.0067992	0.1484705	19.0945148	-0.0190294	2.1377332	0.0021045	0.0221433	0.0000390	3.8783867	4.3162045	-0.0171786	0.1278165	-0.0119618	-0.3522736	-0.0501855	-0.3270764	-0.1004921	-0.5133076	2.0736780	2.2502327	-0.0073879	0.0070676	-2.4900069	-0.0522900	-0.3492197	-0.1005311	-0.4981292	2.1899190	2.4300070	0.0097907	0.4014700	0.7360508	0.5683194	-0.3505180	0.8753148	0.3406741	0.4917848	-0.5732749	0.4801802	-0.4550385	0.7722272	0.2730940	0.2489859	0.2376962	1.3587183	1.0895698	0.9857153	1.0231543	1.0398037	1.0152543	0.5357812	0.0645478	0.5793087	-0.0014692	0.0180000	12.603136	0.5536283	0.0005389	0.000300	127.41681	1.7064546	-10.87862	-11.8201790	6	7	0.0860347	0.0544361	4.975796	1317.000	9931.672	58	98	183	0.0204794	0.7573612	0.3395441	1.832904	69.16074	6
4_26-In-012	d1974_1978	2572937	1203693	calibration	moderate	1	1	6.200000	6.147128	5.603502	5.904355	1.569093	1.543057	5.953919	6.990917	1.565405	1.563151	4.000320	11.330072	0.0011398	0.0021498	0.0017847	0.1112066	-9.1396294	0.0039732	-0.4178924	0.0009509	0.0431735	0.0034232	0.7022317	0.4170935	-0.0026431	-0.0183221	0.0015183	-0.2168447	-0.0079620	0.0053904	-0.0091239	-0.0110896	0.3974485	0.2292406	-0.0013561	-0.0024548	0.2010477	-0.0089129	-0.0377831	-0.0125471	-0.0052359	0.4158890	0.2700820	0.0012870	0.6717541	0.4404107	-0.6987815	-0.1960597	-0.3866692	-0.7592779	-0.9633239	-0.3006475	-0.9221049	-0.3257418	-0.9502072	0.2305476	0.2182523	0.1434273	0.7160403	0.5758902	0.5300468	0.5107915	0.5744110	0.4975456	0.2001768	0.1311051	0.4620202	0.0340407	-0.0145804	7.100000	0.4850160	0.0000124	0.000000	143.41533	0.9372618	22.10210	0.2093917	6	7	0.0737963	3.6830916	4.986864	1315.134	9935.438	58	98	183	0.0048880	0.7978453	0.4455501	1.981526	63.57096	6
4_26-In-014	d1974_1978	2573374	1203710	validation	well	0	0	6.600000	6.754607	7.200000	7.151129	1.569213	1.542792	4.856076	6.964162	1.562499	1.562670	4.000438	42.167496	0.0000000	0.0008454	0.0021042	0.3710849	-0.9318936	-0.0371234	-0.0289909	0.0029348	-0.1056513	0.0127788	1.5150748	0.2413423	0.0020990	-0.0706228	-0.0113604	-0.0272214	-0.0301961	-0.0346193	-0.0273140	-0.0343277	0.8245047	0.1029889	-0.0041158	0.0257630	0.0017695	-0.0331309	0.0710320	-0.0400928	0.0529446	0.8635767	0.1616543	-0.0062147	0.4988544	0.4217250	-0.8485889	-0.8836724	-0.8657616	-0.8993938	-0.4677161	-0.5735765	-0.4998477	-0.4121092	-0.4782534	0.3859352	0.2732429	0.1554769	0.8482135	0.8873205	0.8635756	0.9015982	0.8518201	0.5767300	0.2149791	0.3928713	0.8432562	0.0686932	-0.0085602	8.303085	0.3951114	0.0000857	0.000100	165.80418	0.7653937	-20.11569	-7.7729993	6	7	0.0859686	0.0075817	5.285522	1315.160	9939.923	58	98	183	0.0064054	0.4829135	0.4483251	2.113142	64.60535	6
4_26-In-015	d1968_1974_ptf	2573553	1203935	validation	moderate	0	1	6.272715	6.272715	6.718392	7.269008	1.570359	1.541979	4.130917	6.945287	1.550528	1.562685	4.000948	5.479310	0.0054557	0.0043268	0.0045225	0.3907509	4.2692256	0.0378648	0.6409346	0.0022611	-0.1020419	0.0161510	3.6032522	1.8169731	0.0346340	0.0476020	0.0378154	0.2968794	-0.0179657	-0.0137853	-0.0146946	0.0060875	1.4667766	0.9816071	0.0337645	-0.0000494	-0.3440553	-0.0202268	0.0882566	-0.0308456	0.0929077	2.6904552	1.0218329	-0.0008695	0.6999696	0.3944107	-0.8918364	-0.7795515	-0.8864348	-0.4249992	0.5919228	0.4304937	0.4614536	0.6559467	0.4574654	0.4330348	0.3299487	0.1889674	1.2301254	1.8937486	1.2098556	1.5986075	1.2745584	2.7759163	0.5375320	0.3582314	1.1426100	0.3005829	0.0061576	10.110727	0.5134069	0.0002062	0.000200	61.39244	1.0676192	-55.12566	-14.0670462	6	7	0.0650000	0.0007469	5.894688	1315.056	9942.032	58	98	183	0.0042235	0.6290755	0.3974232	2.080674	61.16533	6
4_26-In-016	d1968_1974_ptf	2573310	1204328	calibration	poor	0	1	6.272715	6.160700	5.559031	5.161655	1.569434	1.541606	2.030315	6.990967	1.563066	1.552568	4.000725	13.499996	0.0000000	0.0001476	0.0003817	0.1931891	-0.1732794	-0.1602274	0.0318570	-0.0035833	-0.1282881	0.0003549	1.5897882	0.8171870	-0.0123340	0.0400775	-0.0813964	0.0100844	-0.0049875	0.0320331	-0.0049053	0.0374298	0.7912259	0.3455668	-0.0059622	0.0788309	-0.0217726	-0.0014042	0.1603212	-0.0052602	0.0867119	1.0207798	0.6147888	0.0063718	0.3157751	0.5292308	-0.8766075	0.8129975	0.5905659	0.1640853	0.5820994	0.6325440	0.8054439	0.7448481	0.6081498	0.3688371	0.2607146	0.1763995	1.0906221	1.0418727	0.8515157	1.2106605	0.8916541	1.2163279	0.4894866	0.2049688	0.7156029	-0.0910767	0.0034276	9.574804	0.3864355	0.0001151	0.000525	310.05014	0.1321367	-17.16055	-28.0693741	6	7	0.0731646	0.0128017	5.938320	1315.000	9940.597	58	98	183	0.0040683	0.6997021	0.4278295	2.041467	55.78354	6

2.4 More data wrangling

Now, not all our covariates may be continuous variables and therefore have to be encoded as factors. As an easy check, we can take the original corvariates data and check for the number of unique values in each raster. If the variable is continuous, we expect that there are a lot of different values - at maximum 1052 different values because we have that many entries. So, let’s have a look and assume that variables with 10 or less different values are categorical variables.

Code

vars_categorical <- df_covars |> 
  
  # Get number of distinct values per variable
  dplyr::summarise(dplyr::across(dplyr::everything(), ~dplyr::n_distinct(.))) |> 
  
  # Turn df into long format for easy filtering
  tidyr::pivot_longer(
    dplyr::everything(), 
    names_to = "variable", 
    values_to = "n"
    ) |> 
  
  # Filter out variables with 10 or less distinct values
  dplyr::filter(n <= 10) |>
  
  # Extract the names of these variables
  dplyr::pull('variable')

cat("Variables with less than 10 distinct values:", 
    ifelse(length(vars_categorical) == 0, "none", vars_categorical))

Variables with less than 10 distinct values: geo500h1id

Now that we have the names of the categorical values, we can mutate these columns in our data frame using the base function as.factor():

Code

df_full <- df_full |> 
  dplyr::mutate(dplyr::across(all_of(vars_categorical), ~as.factor(.)))

2.5 Checking missing data

We are almost done with our data preparation, we just need to reduce it to sampling locations for which we have a decent amount of data on the covariates. Else, we blow up the model calibration with data that is not informative enough.

Code

# Get number of rows to calculate percentages
n_rows <- nrow(df_full)

# Get number of distinct values per variable
df_full |> 
  dplyr::summarise(dplyr::across(dplyr::everything(), 
                                 ~ length(.) - sum(is.na(.)))) |> 
  tidyr::pivot_longer(dplyr::everything(), 
                      names_to = "variable", 
                      values_to = "n") |>
  dplyr::mutate(perc_available = round(n / n_rows * 100)) |> 
  dplyr::arrange(perc_available) |> 
  head(10) |> 
  knitr::kable()

variable	n	perc_available
ph.30.50	856	81
ph.10.30	866	82
ph.50.100	859	82
timeset	871	83
ph.0.10	870	83
dclass	1006	96
site_id_unique	1052	100
x	1052	100
y	1052	100
dataset	1052	100

This looks good, we have no variable with a substantial amount of missing data. Generally, only pH measurements are lacking, which we should keep in mind when making predictions and inferences. Another great way to explore your data, is using the {visdat} package:

Code

df_full |> 
  dplyr::select(1:20) |>   # reduce data for readability of the plot
  visdat::vis_miss()

Alright, we see that we are not missing any data in the covariate data. Mostly sampled data, specifically pH and timeset data is missing. We also see that this missing data is mostly from the same entries, so if we keep only entries where we have pH data - which is what we are interested in here - we have a dataset with pracitally no missing data.

2.6 Save data

Code

if (!dir.exists(here::here("data"))) system(paste0("mkdir ", here::here("data")))
saveRDS(df_full, 
        here::here("data/df_full.rds"))